线性代数笔记(十二)——图和网络
这一讲作为第一部分的最后一节内容,主要着重于描述线性代数的应用。
图和网络
有向图
给定一个有向图:4节点,5条边
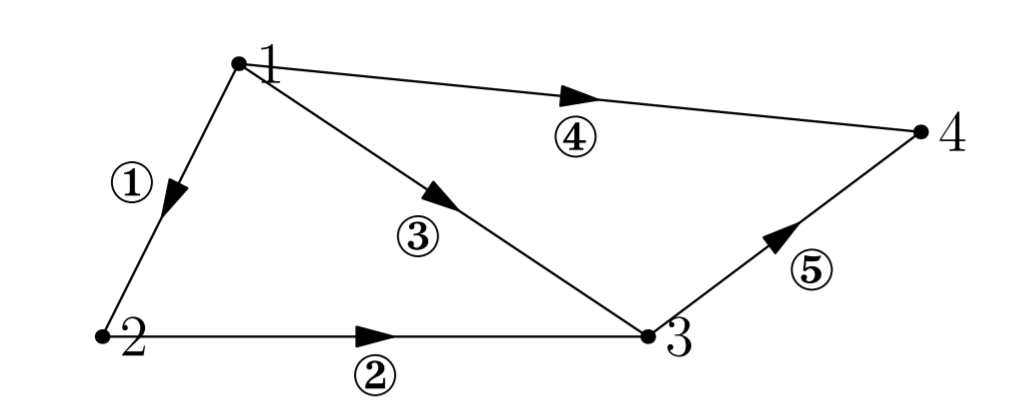
可以用如下方式来抽象描述: \[ \begin{array}{c | c c c c} & node_1 & node_2 & node_3 & node_4 \\ \hline edge_1 & -1 & 1 & 0 & 0 \\ edge_2 & 0 & -1 & 1 & 0 \\ edge_3 & -1 & 0 & 1 & 0 \\ edge_4 & -1 & 0 & 0 & 1 \\ edge_5 & 0 & 0 & -1 & 1 \end{array} \]
写成\(5\times 4\)矩阵来表示如下: \[ A=\begin{bmatrix} -1 & 1 & 0 & 0 \\ 0 & -1 & 1 & 0 \\ -1 & 0 & 1 & 0 \\ -1 & 0 & 0 & 1 \\ 0 & 0 & -1 & 1 \end{bmatrix} \]
这种矩阵叫做关联矩阵,其中每一列代表一个节点,每一行代表一条边(正负代表方向)。关联矩阵一般是稀疏阵,因为每一行只有两个非零元素。通过观察前三行,可以看出这三个行向量线性相关,而实际上,它的物理意义就是这三个向量(三条边)可以形成回路。
\(A\)的零空间
矩阵\(A\)的零空间可以通过解\(Ax=0\)来得到,有: \[ Ax= \begin{bmatrix} -1 & 1 & 0 & 0 \\ 0 & -1 & 1 & 0 \\ -1 & 0 & 1 & 0 \\ -1 & 0 & 0 & 1 \\ 0 & 0 & -1 & 1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix}=0 \]
展开得: \[ \begin{bmatrix} x_2-x_1 \\ x_3-x_2 \\ x_3-x_1 \\ x_4-x_1 \\ x_4-x_3 \end{bmatrix}= \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix} \]
引入矩阵的实际意义:将\(x=\begin{bmatrix}x_1 & x_2 & x_3 & x_4\end{bmatrix}\)视为各节点电势,则式子中的诸如\(x_2-x_1\)的元素,可以看做该边上的电势差。容易看出其中一个解\(x=\begin{bmatrix}1\\ 1\\ 1\\ 1\end{bmatrix}\),即等电势情况,此时电势差为\(0\)。化简\(A\)易得\(rank(A)=3\),所以其零空间维数应为\(n-r=4-3=1\),即\(\begin{bmatrix}1\\1\\1\\1\end{bmatrix}\)就是其零空间的一组基。
Q: 那么以电势为例,零空间的物理意义是什么呢? A: 电势差和电流的形成之间有着直接关系,\(b=0\)说明我们求解的情况是各个边上都没有电流(或者说电势差)的情况,而我们最后所得到的解就意味着,当各点电势相等时,边上电流(电势差)为零,符合我们的常识。而这就是零空间的物理意义。
\(A\)的左零空间
\(A\)的左零空间是什么呢?或者说\(A^T\)的零空间是什么呢?即求\(A^Ty=0\): \[ A^Ty=0= \begin{bmatrix} -1 & 0 & -1 & -1 & 0 \\ 1 & -1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & -1 \\ 0 & 0 & 0 & 1 & 1 \end{bmatrix} \begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ y_4 \\ y_5 \end{bmatrix}=\begin{bmatrix} -y_1-y_3-y_4 \\ y_1-y_2 \\ y_2+y_3-y_5 \\ y_4+y_5 \end{bmatrix}= \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \end{bmatrix} \]
接着说上文提到的的电势差,引入\(y\)的实际物理意义:即各边上的电流。电流和电势差的关系服从欧姆定律:边上的电流值是边上电势差的倍数,这个倍速就是边的电导,亦即电阻的倒数,通常我们把这个常数视为一个系数矩阵记为\(C\)。于是,矩阵\(C\)就将电势差与电流联系了起来: \[ y=\begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ y_4 \\ y_5 \end{bmatrix}=C\begin{bmatrix} x_2-x_1 \\ x_3-x_2 \\ x_3-x_1 \\ x_4-x_1 \\ x_4-x_3 \end{bmatrix} \]
实际上\(A^Ty=0\)阐释的就是“基尔霍夫电流定律”(KCL),基尔霍夫电流定律是一个平衡方程,守恒定律,它说明了流入等于流出,电荷在结点上不会积累。
对于\(A^T\),根据上文得出其零空间的维数是\(2\),则零空间的基应该有两个向量。假设\(y_1=1\),也就是令\(1\)安培的电流在边\(1\)上流动,由图看出\(y_2\)也应该为\(1\),再令\(y_3=-1\),也就是让\(1\)安培的电流流回节点\(1\),得出\(y_4=y_5=0\);
得到一个符合KCL的向量\(\begin{bmatrix}1\\ 1\\ -1\\ 0\\ 0\end{bmatrix}\),代回方程组发现此向量即为一个解,这个解发生在节点\(1,2,3\)组成的回路中,该解即为零空间的一个基。
如法炮制可以得出另一个基向量:\(\begin{bmatrix}0\\ 0\\ 1\\ -1\\ 1\end{bmatrix}\),这实际上是节点\(1,3,4\)构成的回路。
如此,我们得到\(N(A^T)\)的一组基为\(\begin{bmatrix}1\\ 1\\ -1\\ 0\\ 0\end{bmatrix}\quad\begin{bmatrix}0\\ 0\\ 1\\ -1\\ 1\end{bmatrix}\)。
节点\(1,2,3,4\)构成的大回路实际上是两个基向量回路的叠加。
\(A\)的行空间
亦即\(A^T\)的列空间,方便起见我们直接计算\(A^T\)的列空间: \[ A^T= \begin{bmatrix} -1 & 0 & -1 & -1 & 0 \\ 1 & -1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & -1 \\ 0 & 0 & 0 & 1 & 1 \end{bmatrix} \]
显然,\(A^T\)的主列为第\(1,2,4\)列,对应在图中就是边\(1,2,4\),可以发现这三条边没有组成回路(换句话说,线性无关等价于没有回路)。由\(4\)个节点与\(3\)条边组成的图没有回路,就表明\(A^T\)的对应列向量线性无关,也就是(\(nodes-1\))条边线性无关。
没有回路的图叫作树。
再看左零空间的维数公式:\(dim N(A^T)=m-r\),左零空间的维数就是相互无关的回路的数量,于是得到\(loops=edges-(nodes-1)\),整理得: \[ nodes-edges+loops=1 \]
此等式对任何图均有效,任何图都有此拓扑性质,这就是著名的欧拉公式: \[ 节点数-边数+最小回路数=1 \]